家庭教師ファースト教育コラム大学受験
家庭教師ファースト教育コラム大学受験
家庭教師ファースト教育コラム大学受験
理系のみなさんは、理科の選択科目で化学と物理or生物を選ぶ人が大半です。
化学はほぼ全員が選択するとして、生物か物理かといった選択を迫られたとき(工学部では、物理は必修であることが多いです)、「物理って難しそう」というイメージを持っている人が多いのではないでしょうか。
確かに導入は難しいと感じることが多いですが、コツをつかめば、暗記量を少なくして高得点を期待することが出来る科目でもあります。
カリキュラム的に、高１で物理基礎を習い、高２高３で物理を習うことになりますが、内容のわりに授業時間が短かったり、進度が間に合わなかったりと演習不足に陥りやすく、得点が伸び悩むことが多い科目です。
筆者は、公立高校卒ですが、電磁気を習い終わったのが高3の11月で、原子物理はセンター試験後に習い終わり、学校での演習の授業はありませんでした。
難しそうでカリキュラム的に間に合わなさそうという悪条件の整った物理ではありますが、今回は公立高校卒・現役医大生の筆者が、そんな物理の攻略方法をお伝えしていきます。
なお、家庭教師ファーストには私も含め現役大学生や社会人・プロの家庭教師も多数在籍しています。
家庭教師を付けて相談してみる、というのも一つの手かもしれません。
大学受験といえば、「英語と数学で決まる」という格言？があります。
では、理科は相対的に重要ではないのでしょうか。
いいえ。そんなことはありません。
上記の格言は、高１高２の夏あたりまでが対象です。
英数は、習う範囲が膨大かつ総合的な完成度の高さを求められる科目なので、早期から継続的に対策する必要があるので、このような格言があります。
理科は、比較的短期間(それでも1年近くは必要)で仕上がるため、高１から必死になる必要は無く、定期テスト対策がメインで問題ないですが、高２の秋以降は理科をどんどんやっていかなければなりません。
物理に限らず、理科はカリキュラムがギリギリの学校が多く、演習不足のままでは点数が思うように取れません。
しかし、国公立二次試験や私立の一般入試問題を見てみると、英数に比べて、比較的量が多く簡単な問題が多いのが特徴です。
つまり、理科の得点力で合計点に大きな差が生まれます。
この差こそが、合否に直結するため、英数がある程度できているという前提のもとでは、理科が合否を決めるといっても過言ではありません。
物理は、学習順に力学、熱力学、波動、電磁気、原子物理の5分野から構成されています。
入試に出題される割合としては、力学：熱力学：波動：電磁気：原子物理＝30：15：20：30：5といったところです（大学によって差はあります）。
しかし、重要度で言うと、力学が60くらいを占めます。
これは、全ての分野において力学が基本的な考え方としてとても重要だからです。
ここから先は、時期別に物理との向き合い方をお伝えしていきます。
高２の夏までは、冒頭にもお伝えしましたが、英数を頑張りましょう。
高２の夏までは模試に理科がないため、著しく理科が欠落していても気づきにくいですが、気にしなくて大丈夫です。
この時期までに英数を頑張っていると、後々高３で理科に割く時間を増やすことができるようになります。
とはいっても、無策でいてはいけません。
のちに分野別の攻略法で詳しくお伝えしますが、この時期は物理で最も重要な力学を習います。
普段の勉強は英数に譲る分、テスト1週間前からは物理に時間を割きましょう。
センサー、セミナー、リードアルファといった教科書傍用問題集を3周ほどこなしてテストで高得点を目指しましょう。
テストが終わると、しばらくすると忘れてしまうかもしれませんが、模試もないのでとりあえず放置で大丈夫です。
とにかく定期テスト対策に全身全霊で取り組んでください。
一度しっかり完成させておくと、入試問題集を解き始めたときの記憶の復元がかなり楽になります。
定期テストの範囲に教科書傍用問題集が全て入っていれば、テスト対策のみで大丈夫なのですが、多くの高校は、定期テストには「STEP3」や「応用問題」といった部分を試験範囲から除外していることがあります。
定期テスト対策の時には、取り組まなかったとしても、テスト後にトライしておくことが重要です。
この、教科書傍用問題集の「STEP3」や「応用問題」に当たる部分が、入試基礎として教科書レベルから本格的な入試問題への橋渡しとしてかなり重要になります。
「ＳＴＥＰ２」や「基本問題」、「標準問題」といった項目では、数値を与えて計算させてきますが、「ＳＴＥＰ３」や「応用問題」では、文字のまま計算させてくるという違いがあります。
実際の入試問題で数値計算をさせてくる例はほとんどありません。
よって、「ＳＴＥＰ３」や「応用問題」で文字の計算に慣れておくと、入試問題での計算が速く正確になります。
具体的には、質量mで約分出来たり、共通因数でくくると簡単に求められたりするケースが多いです。
高２の秋からは、それまでよりも少し理科のウエイトを増やしていきましょう。
定期テスト対策として教科書傍用問題集を「STEP3」や「応用問題」といった範囲まで全てこなしておきましょう。
余裕のある人は、力学の入試問題を解き始めましょう。
入試問題集を解き始めるのは高３からでも良いのですが、高２の秋冬から模試に理科が入ってくるので、模試での得点アップのために力学だけでも入試問題集を解き始めることをお勧めします。
入試問題集としては数研出版の重要問題集のＡ問題や良問の風くらいでかまいません。
いきなり、名門の森や難問題の系統とその解き方などといった最難関問題集に手を出してはいけません。
高２の夏まで物理に勉強時間をさけなくて、教科書傍用問題集の応用を解けていなかった人は、解いておきましょう。
繰り返しになりますが、このレベル感が入試基礎として極めて重要なレベルなので、ここを省略して高３からいきなり入試問題集に飛びつくといった愚策は取らないでください。
この入試基礎のレベルは、高２の模試で出題されるレベルに相当します。
既習範囲の入試基礎まで終えていれば、理想的な高２です。
高３の春に習う電磁気は力学と並んで物理の最重要分野なので、じっくりと時間をかけて習得してください。
力学よりもイメージをつかみにくいので取り組みにくいですが、諦めると物理で大幅な点数ダウンにつながってしまうので、他の分野の入試問題集を解くのをやめてでも電磁気に専念しましょう。
教科書傍用問題集をきっちり仕上げます。
夏休みに入ると、力学、熱力学、波動の入試問題集を徹底的に演習します。
重要問題集をＢ問題まで含めて終わらせることを目標とします。
最難関を目指す人は、名門の森や難問題の系統とその解き方などの最難関問題集に手を出してもいいと思います。
電磁気は、習った範囲までの入試問題集を解ければ、かなり上出来です。
模試は、電磁気が全範囲入りますが、学校によって(特に公立高校)では、習い終わっていなくて、記述模試はボロボロかもしれませんが、焦る必要はありません。
高３の秋以降、原子物理を習っていきます。
電磁気の最後の方である交流や、原子物理は出題頻度が低いですが、注意すべきポイントがあります。
それは、復習が難しいということです。
力学、熱力学、波動であれば、高２の冬休みや高３の夏休みに時間をかけて復習することが可能ですが、電磁気と原子物理は初めて習うときが模試の多い時期であったり、入試前であったりと、時間を取って復習することが難しいです。
よって、上述のように、初めて習ったときにじっくりと時間をかけて理解してください。
さて、ここまでは時期別におおまかな対策の流れを説明してきました。
ここからは、各分野別の対策をお伝えしていきます。
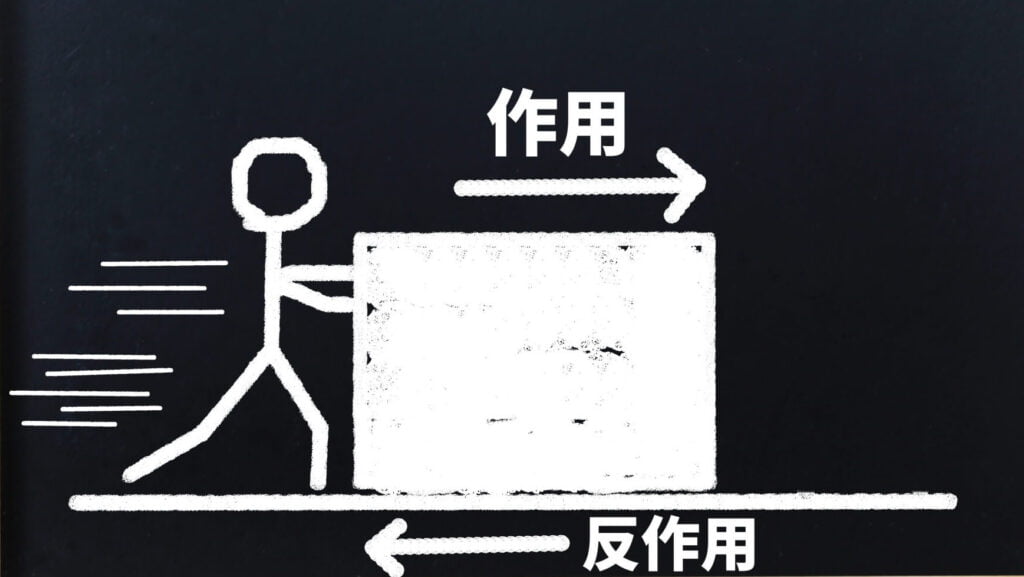
力学は、大学受験において最も大切な分野です。
また、他の分野においてもつり合いや運動方程式といった概念が登場することもしばしばあるため、力学が苦手なままだと、全ての分野の足かせになるため、時間をかけてでも習得する必要があります。
力学は、単元数が多いですが、重要な単元はわずか3単元です。
それは、「つりあい」、「運動方程式」、「エネルギー保存則」です。
この3つから、摩擦、仕事、衝突、円運動、単振動などが付随していきます。
なので、この3つをしっかり仕上げたのちに、これらの単元に入っていきましょう。
逆に、円運動が分からなければ、円運動自体があまりわかっていないのではなく、実は運動方程式の理解に問題があるかもしれないと推測することも出来ます。
力学の問題は、図を描いて下さい。
図を描いた後、働く力を図示してください。
働く力を図示した後、着目した物体が静止または等速直線運動をしていればつり合いの式、等速直線運動以外で動いていれば、運動方程式を立てることになります。
実際に、お手元の問題集の摩擦のページを開いて、図を描いて、働く力を図示してみてください。
どうでしょうか。
正確に図示できた人は、そんなに多くないと思います。
摩擦の力を逆向きにしてしまった人も多いのではないでしょうか。働く力の図示は、慣れていなければ難しい作業です。
しかし、働く力の図示さえ正確にできれば、あとは、つり合いの式か運動方程式を立式して連立すればほとんどの問題は解けます。
なので、図を描いて働く力の図示を正確に行う訓練をしてください。
慣れれば、誰でもすぐできます。
このときに、なんとなく適当に働く力の図示をするのではなく、何が何を押す力かをイメージしながら図示していきましょう。
図を描くときは、小さく描かず大きめに描いて下さい。
ややこしめの入試問題であれば、ノートのページ半分くらいを使ってもいいです。
力の図示がかなり多くなってくると、小さな図だと見にくくてミスを誘発したり、復習する気が失せたりします。
熱力学は、化学の気体の状態方程式とかぶっているので、実際には勉強していないのに、勉強した気分になってしまいがちなので注意が必要です。
熱力学自体は、単元が少なく、特筆すべき事項はありません。
期待の分子運動論は力学の復習ですし、密封気体の圧力変化によるピストンの運動も半分くらい力学の守備範囲です。
熱力学特有の問題といえば、状態変化についての問題です。
状態変化が苦手な人向けに、数学的に解決する方法をご紹介いたします。
熱力学の公式を列挙します。
⊿Qin=⊿U(=nCv⊿T)+Wout(=P⊿V)
PV=nRT
PVɤ=一定（ɤ=CpCv）
この式の連立方程式で解くことができます。
例えば、断熱変化の時、内部エネルギーの変化が気体のされた仕事と等しいと物理的にイメージできなくても、熱力学の第一法則で、
⊿Qin=0と分かれば、機械的に、
⊿U=-Woutと導くことができます。
力学では、力の図示により、視覚的に減少をイメージしやすいですが、熱力学は、力の図示ができない問題がしばしばあるため、現象を頭の中でイメージして解けなくても、公式から数学的に導く方が速くて正確なことが多いです。
基本的に物理は、図示して現象を視覚的にとらえることを推奨していますが、熱力学は数学的に解くことを提唱します。
私が上記に挙げた熱力学第一法則には、in outなどの添え字があります。
これには意味があって、符号ミスを未然に防いでくれるという役割があります。
熱力学の単元では、仕事をした、された、熱量を吸収した、放出した、気体が仕事をした、仕事をされた、といった能動態か受動態かでプラスマイナスが入れ替わるものが非常にたくさんあります。
添え字をつけることで、自分は何を求めているのかを視覚的に確認できます。
答えが負の値になれば、受動と能動を入れ替えれば良いです。
波動は、ドップラー効果と干渉が重要単元です。
力学的要素が全くなく、新ジャンルですが、こちらも図を描いておきましょう。
ドップラー効果の問題は、公式を覚えているだけでは全然解けません。
なぜなら、公式の導出過程から設問になるからです。
公式の導出過程は、1秒間に出たf個の波が何メートルの間に広がっているのか、観測者が聞く波の数、の2点がとても重要です。
これらに留意して自分で導出できるようになっていれば、ドップラー効果の問題はほとんど解くことができるようになります。
素材がたくさんあってややこしいですが、ヤングの実験、回折格子、薄膜、くさび形、ニュートンリング、マイケルソン干渉計、のいずれにおいても光路差から明暗の条件の導出までできるようにしておきましょう。
明暗の条件の導出の過程では、誘導付きで微少量を無視することによる近似を行うことが多いので、一通り慣れておきましょう。
図を描くことで光路差が視覚的に分かったり、縞の間隔を考察させる問題も視覚的に分かるようになったりします。
難しい問題になればなるほど式だけで押し通すことは難しいので、図を描きましょう。
共通テストや一部の私立大学で好んで波動の減少を日常生活に絡めた問題が出題されることがあります。
夜間は遠くの音がよく聞こえる理由（地表と上空の気温差における音波の屈折）、虹が見える理由（太陽光が水滴で2回の屈折と1回の反射）、昼間は太陽の周りが白っぽく見えて、夕方は太陽の周りが赤く見えて空が青く見える理由（光の散乱）、といった現象を、屈折、散乱、反射などの物理用語を使って詳しく説明することが出来る必要があります。
このほかにも回折、乱反射、偏光などについても日常生活と絡めて説明できるようになっておくとよいです。
いずれも、教科書に具体例が記載されていますので、一度通読しておくことをお勧めします。
電磁気は、コンデンサーと電磁誘導が山場です。
コンデンサーは、中学まででは登場しない新しい物体です。
1つのコンデンサーの極板に注目して電荷や電気力線、電位差に注目する設問と、コンデンサーを含む複雑な回路についての設問の2種類があります。
前者は、極板間隔を広げたり誘電体の挿入をしたりしますが、コンデンサーに気を取られ過ぎてはいけません。
そのときに電源とつないだままなのか、それとも電源から離しているのかが大切です。
後者は、各極板における電位、電荷が大切になります。
中学の頃は、回路といえば電流と抵抗のイメージが強かったかもしれませんが、高校では各導線における電位が大切です。
等電位の部分をマーカーで塗っていくと、どこが等電位なのかわかりやすくなります。
現象自体は中学の頃に知っているかと思いますが、高校物理では大きな山場です。
フレミングの左手の法則からわかるように、電流、磁界、力は3点セットになります。
電流磁界に加えて、力も関わってくるので、力学が大きく関わってきます。つり合い、運動方程式、エネルギーと仕事などが深く関わってきます。
磁界の単元で、WbやＴといった単位が登場しますが、これらは、公式によって電流や力とつながっています。
ということは、磁界特有の単元は、実は、なじみ深い単位で表すことができます。これは、次元解析という方法で、基本単位で組立単位を表すことを指します。
この次元解析は、入試問題として出題される頻度は高くはありませんが、計算ミスの防止に役立つので知っておきましょう。
どのように役立つのか、例示します。
mv+mv²という計算を見て何も思わないかもしれません。
しかし、mvは運動量を表し、mv²はエネルギーを表し、異なる単位を示しています。
異なる単位の加減はできませんから、この時点で、どちらかに計算ミスがあることが分かります。
このように、単位について詳しくなっていると、計算ミスに気付きやすくなります。
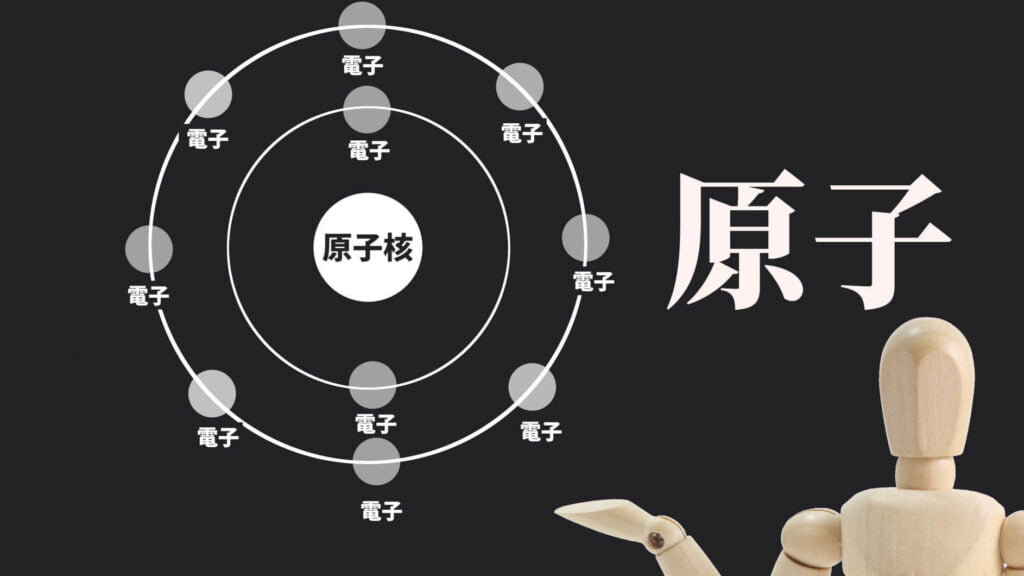
原子物理は、本気で取り組むとかなり難しいです。
はっきり言って高校物理の手に負えません。
なので、重要部分だけサラッとこなしてしまいましょう。
光電効果、Ｘ線の粒子性の確認としてのコンプトン効果、Ｘ線の波動性の確認としてのブラッグの反射条件、ボーアの水素原子モデルから量子条件の導出、エネルギー準位、核融合核分裂の項目を抑えておきましょう。
たくさん列挙してしまいましたが、波動性は波動の知識、粒子性は力学の知識が役に立ちます。
ボーアの量子条件の導出には円運動の知識、核融合核分裂は力学の衝突と分裂が役に立ちます。
公式に加えて少しだけ原子物理特有の概念はありますが、基本的には、背景に今までの努力がありますので、原子物理までの勉強をしっかりこなしていれば、必死になって取り組まなくても大丈夫です。
以上、物理の勉強法について説明してきました。
基本的には、教科書傍用問題集をこなしつつ、高２の後半か高３から入試問題集を解いていけば、公立高校の遅い進度であっても理想的なペースです。
各分野の特徴を掴んで学習していけば、化学ともバランスよく勉強していけます。
図を描く習慣を身に着け、力学に重点を置き、各分野とも他の分野と連携している部分は、ラクしつつ取り組んでいきましょう。
入試において理科は得点源ですが、くれぐれも時間をかけ過ぎて「英数」に悪影響を及ぼさないように注意しつつ、効率よく高得点を目指しましょう。
繰り返しになりますが、一人でなかなか対策が進まない場合は、是非私たち家庭教師に相談してください。
時間は有限です。是非後悔のないように最大限の対策をしていきましょう。
現役医大生ライター I
家庭教師ファーストの登録教師。和歌山県立医科大学 医学部に在学中。国立中学受験を経験。学生ながら、指導人数は20名以上。
家庭教師ファースト/株式会社エムズグラント
『質の高いサービスを、良心的な価格で』をモットーに、全国で20年以上家庭教師を紹介しています。実際に担当する教師による体験指導受付中。教育に関する相談もお気軽に。
学習の家庭教師：https://www.kyoushi1.net/
スポーツの家庭教師：https://www.taiiku-sports.com/
